Линейная модель парной регрессии.

По территориям региона приводятся данные за определенный период.
Таблица 1

1. Постройте поле корреляции, сформулируйте гипотезу о форме связи
2. Найдите ковариацию и сделайте вывод о виде связи между х и у.
3. Найдите средние квадратические отклонения
4. Найдите уравнение линейной регрессии

Решение
1. Для выяснения характера связи между средней заработной платой и потребительскими расходами данным строится поле корреляции (тип диаграммы - график).

По графику видно, что точки выстраиваются в некоторую прямую линию. Следовательно, связь между средней зара-ботной платой и потребительскими расходами линейная.
2. Для дальнейших вычислений в составленную таблицу добавьте столбец "ху" и строку "ср.знач.", заполнив их зна-чениями, вычисленными соответствующим образом.

Т.о., получены средние значения х, у, ху (обозначаемые
Тфблица 2




Положительное значение ковариации говорит о прямой связи между факторами х и у, т.е. с возрастанием х возрастает у, с убыванием х убывает у.

В таблицу вносятся соответствующие дополнения
Таблица 3


Получены следующие значения
Таблица 4


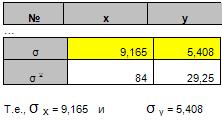
4. По построенному полю корреляции был сделан вывод о том, что связь между средней заработной платой и потреби-тельскими расходами линейная. Для построения уравнения линейной регрессии удобно воспользоваться Таблицей 5
Таблица 5

Уравнение линейной регрессии имеет вид


Необходимо найти параметры a, b.
Воспользовавшись формулами и рассчитываются параметры линейного уравнения парной регрессии:


Т.о., с увеличением средней заработной платой на 100 ден. единиц потребительские расходы увеличиваются на 58 ден. единиц